확장 유클리드 알고리즘으로 모듈러 연산 역산하기

 

유클리드 알고리즘으로 as+bt=gcd(a,b)를 만족하는 정수 s, t 짝을 찾아낼 수 있다.

초기식은 s0=1, s1=0 ,t0=0, t1=1,  r0=a, r1=b으로

를 표를 만들어 대입하면 보기 쉬워진다.

	si	ti	ri	qi
i=0	1	0	a
i=1	0	1	b	floor(a/b)
			a mod b

15s+6t=3를 예시로 값을 각각 넣어보면

	si	ti	ri	qi
i=0	1	0	a=15
i=1	0	1	b=6	floor(15/6)=2
			15 mod 6 =3

si ti의 1 0 ,0 1은 그대로 a는 15 b는 6를 넣고 각각 대입해준다.

	si	ti	ri	qi
i=0	1	0	a=15
i=1	0	1	b=6	floor(15/6)=2
i=2	1-0*2=1	0-1*2=-2	15 mod 6 =3	floor(6/3)=2
i=3			6 mod 3=0

색칠되어있는 곳을 바탕으로 위의 식에 대입해 값을 구한다.

값을 구하다보면 ri의 값이 0이되는데 식이 나누어떨어지는 s t값을 구했다는 뜻이다.

15s+6t=3 식에 ri가 0이 될때의 si ti 값을 넣어보면 15*1-12=3으로 맞는것을 알수있다.

 

위의 개념을 응용해

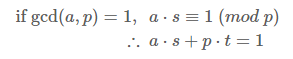
나머지 연산 곱셈의 역원을 구할때의 식으로 s값을 찾을 수 있게된다.

초기값으로는

s를 구하기 위해서는 s1 = 1, s2 = 0을 설정

t를 구하기 위해서는 t1 = 0, t2 = 1을 설정

 

s와 t의 계산에서는 r1 ÷ r2의 몫인 q를 사용한다.

s = s1 - q x s2,

t = t1 - q x t2로 계산하고 a, b의 최대 공약수가 나오면 멈추면 된다

 

a*s+b*t=1을 이용해

 

 

ctf문제로 예시를 들어보면

a1배열값에 0xfb를 곱해주고 (unsigned int8)값으로 모듈러연산을 하게 된다.

a1배열의 값*0xfb%256=byte_140003000배열의 값

이를 그대로

(0xfb*s)%256*t=1을 이용해 구해보면

 

	si	ti	ri	qi
i=0	1	0	256(mod 하는값)
i=1	0	1	251(s앞에 있는친구)	1
i=2	1	-1	5	50
i=3	-50	51	1	5
i=4	251	-256	0

51과 -205(b(-256)+(51 나온값))가 역산값으로 나오게 된다.

결과인 140003000값에 51이나 -205를 곱해주고 %256을 하면 a1배열의 값이 나오게 된다.